HJCFIT- maximum likelihood fit of single-channel data:¶
Records at four concentrations fitted simultaneously¶
Some general settings:
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import sys, time, math
import numpy as np
from numpy import linalg as nplin
Load data¶
HJCFIT depends on DCPROGS/DCPYPS module for data input and setting kinetic mechanism:
from dcpyps.samples import samples
from dcpyps import dataset, mechanism, dcplots, dcio
# LOAD DATA: Burzomato 2004 example set.
scnfiles = [["./samples/glydemo/A-10.scn"],
["./samples/glydemo/B-30.scn"],
["./samples/glydemo/C-100.scn"],
["./samples/glydemo/D-1000.scn"]]
tr = [0.000030, 0.000030, 0.000030, 0.000030]
tc = [0.004, -1, -0.06, -0.02]
conc = [10e-6, 30e-6, 100e-6, 1000e-6]
Initialise Single-Channel Record from dcpyps. Note that SCRecord takes a list of file names; several SCN files from the same patch can be loaded.
# Initaialise SCRecord instance.
recs = []
bursts = []
for i in range(len(scnfiles)):
rec = dataset.SCRecord(scnfiles[i], conc[i], tr[i], tc[i])
recs.append(rec)
bursts.append(rec.bursts.intervals())
rec.printout()
Data loaded from file: ./samples/glydemo/A-10.scn
Concentration of agonist = 10.000 microMolar
Resolution for HJC calculations = 30.0 microseconds
Critical gap length to define end of group (tcrit) = 4.000 milliseconds
(defined so that all openings in a group prob come from same channel)
Initial and final vectors for bursts calculated asin Colquhoun, Hawkes & Srodzinski, (1996, eqs 5.8, 5.11).
Number of resolved intervals = 14553
Number of resolved periods = 12322
Number of open periods = 6161
Mean and SD of open periods = 1.288416455 +/- 1.982357659 ms
Range of open periods from 0.030309819 ms to 29.300385504 ms
Number of shut intervals = 6161
Mean and SD of shut periods = 69.358758628 +/- 259.539574385 ms
Range of shut periods from 0.030003177 ms to 6902.281761169 ms
Last shut period = 115.868724883 ms
Number of bursts = 1480
Average length = 6.106142638 ms
Range: 0.039 to 261.102 millisec
Average number of openings= 4.162837838
Data loaded from file: ./samples/glydemo/B-30.scn
Concentration of agonist = 30.000 microMolar
Resolution for HJC calculations = 30.0 microseconds
Critical gap length to define end of group (tcrit) = -1000.000 milliseconds
(defined so that all openings in a group prob come from same channel)
Initial and final vectors for are calculated as for steady state openings and shuttings (this involves a slight approximation at start and end of bursts that are defined by shut times that have been set as bad).
Number of resolved intervals = 15939
Number of resolved periods = 12580
Number of open periods = 6290
Mean and SD of open periods = 1.702516108 +/- 2.243856294 ms
Range of open periods from 0.030157962 ms to 24.172481848 ms
Number of shut intervals = 6290
Mean and SD of shut periods = 70.374920964 +/- 2950.499773026 ms
Range of shut periods from 0.030011479 ms to 194377.349853516 ms
Last shut period = 0.045992190 ms
Number of bursts = 6
Average length = 18819.672168031 ms
Range: 1522.551 to 43719.292 millisec
Average number of openings= 1048.333333333
Data loaded from file: ./samples/glydemo/C-100.scn
Concentration of agonist = 100.000 microMolar
Resolution for HJC calculations = 30.0 microseconds
Critical gap length to define end of group (tcrit) = -60.000 milliseconds
(defined so that all openings in a group prob come from same channel)
Initial and final vectors for are calculated as for steady state openings and shuttings (this involves a slight approximation at start and end of bursts that are defined by shut times that have been set as bad).
Number of resolved intervals = 15085
Number of resolved periods = 10306
Number of open periods = 5153
Mean and SD of open periods = 3.107396297 +/- 3.542747918 ms
Range of open periods from 0.030413088 ms to 46.681848165 ms
Number of shut intervals = 5153
Mean and SD of shut periods = 165.682286024 +/- 6593.143939972 ms
Range of shut periods from 0.030006107 ms to 386315.155029297 ms
Last shut period = 0.060205570 ms
Number of bursts = 12
Average length = 1513.309260650 ms
Range: 0.853 to 5742.387 millisec
Average number of openings= 429.416666667
Data loaded from file: ./samples/glydemo/D-1000.scn
Concentration of agonist = 1000.000 microMolar
Resolution for HJC calculations = 30.0 microseconds
Critical gap length to define end of group (tcrit) = -20.000 milliseconds
(defined so that all openings in a group prob come from same channel)
Initial and final vectors for are calculated as for steady state openings and shuttings (this involves a slight approximation at start and end of bursts that are defined by shut times that have been set as bad).
Number of resolved intervals = 11116
Number of resolved periods = 7948
Number of open periods = 3974
Mean and SD of open periods = 5.501930670 +/- 5.808946772 ms
Range of open periods from 0.031116215 ms to 54.734716301 ms
Number of shut intervals = 3974
Mean and SD of shut periods = 127.277284861 +/- 4903.965950012 ms
Range of shut periods from 0.030000978 ms to 293057.556152344 ms
Last shut period = 2.376423450 ms
Number of bursts = 19
Average length = 1176.491361390 ms
Range: 21.215 to 4484.782 millisec
Average number of openings= 209.157894737
Load demo mechanism (C&H82 numerical example)¶
# LOAD FLIP MECHANISM USED in Burzomato et al 2004
mecfn = "./samples/mec/demomec.mec"
version, meclist, max_mecnum = dcio.mec_get_list(mecfn)
mec = dcio.mec_load(mecfn, meclist[2][0])
# PREPARE RATE CONSTANTS.
# Fixed rates.
#fixed = np.array([False, False, False, False, False, False, False, True,
# False, False, False, False, False, False])
for i in range(len(mec.Rates)):
mec.Rates[i].fixed = False
# Constrained rates.
mec.Rates[21].is_constrained = True
mec.Rates[21].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[21].constrain_args = [17, 3]
mec.Rates[19].is_constrained = True
mec.Rates[19].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[19].constrain_args = [17, 2]
mec.Rates[16].is_constrained = True
mec.Rates[16].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[16].constrain_args = [20, 3]
mec.Rates[18].is_constrained = True
mec.Rates[18].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[18].constrain_args = [20, 2]
mec.Rates[8].is_constrained = True
mec.Rates[8].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[8].constrain_args = [12, 1.5]
mec.Rates[13].is_constrained = True
mec.Rates[13].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[13].constrain_args = [9, 2]
mec.update_constrains()
# Rates constrained by microscopic reversibility
mec.set_mr(True, 7, 0)
mec.set_mr(True, 14, 1)
# Update constrains
mec.update_constrains()
#Propose initial guesses different from recorded ones
initial_guesses = [5000.0, 500.0, 2700.0, 2000.0, 800.0, 15000.0, 300.0, 120000, 6000.0,
0.45E+09, 1500.0, 12000.0, 4000.0, 0.9E+09, 7500.0, 1200.0, 3000.0,
0.45E+07, 2000.0, 0.9E+07, 1000, 0.135E+08]
#initial_guesses = [3687.69, 6091.43, 2467.35, 32621.5, 7061.15, 129984., 1050.69, 20984., 3387.64,
# 0.166224E+09, 20783.8, 6308.02, 2258.42, 0.332447E+09, 31335.4, 144.530, 831.686,
# 0.620171E+06, 554.457, 0.124034E+07, 277.229, 0.186051E+07]
#initial_guesses = mec.unit_rates()
mec.set_rateconstants(initial_guesses)
mec.update_constrains()
mec.printout()
class dcpyps.Mechanism
Values of unit rates [1/sec]:
0 From AF* to AF alpha1 5000.0
1 From AF to AF* beta1 500.0
2 From A2F* to A2F alpha2 2700.0
3 From A2F to A2F* beta2 2000.0
4 From A3F* to A3F alpha3 800.0
5 From A3F to A3F* beta3 15000.0
6 From A3F to A3R gama3 300.0
7 From A3R to A3F delta3 120000.0
8 From A3F to A2F 3kf(-3) 6000.0
9 From A2F to A3F kf(+3) 450000000.0
10 From A2F to A2R gama2 1500.0
11 From A2R to A2F delta2 12000.0
12 From A2F to AF 2kf(-2) 4000.0
13 From AF to A2F 2kf(+2) 900000000.0
14 From AF to AR gama1 7500.0
15 From AR to AF delta1 1200.0
16 From A3R to A2R 3k(-3) 3000
17 From A2R to A3R k(+3) 4500000.0
18 From A2R to AR 2k(-2) 2000
19 From AR to A2R 2k(+2) 9000000.0
20 From AR to R k(-1) 1000
21 From R to AR 3k(+1) 13500000.0
Conductance of state AF* (pS) = 40
Conductance of state A2F* (pS) = 40
Conductance of state A3F* (pS) = 40
Number of open states = 3
Number of short-lived shut states (within burst) = 6
Number of long-lived shut states (between bursts) = 1
Number of desensitised states = 0
Number of cycles = 2
Cycle 0 is formed of states: A3R A3F A2F A2R
forward product = 4.860000000e+18
backward product = 4.860000000e+18
Cycle 1 is formed of states: AF A2F A2R AR
forward product = 3.240000000e+18
backward product = 3.240000000e+18
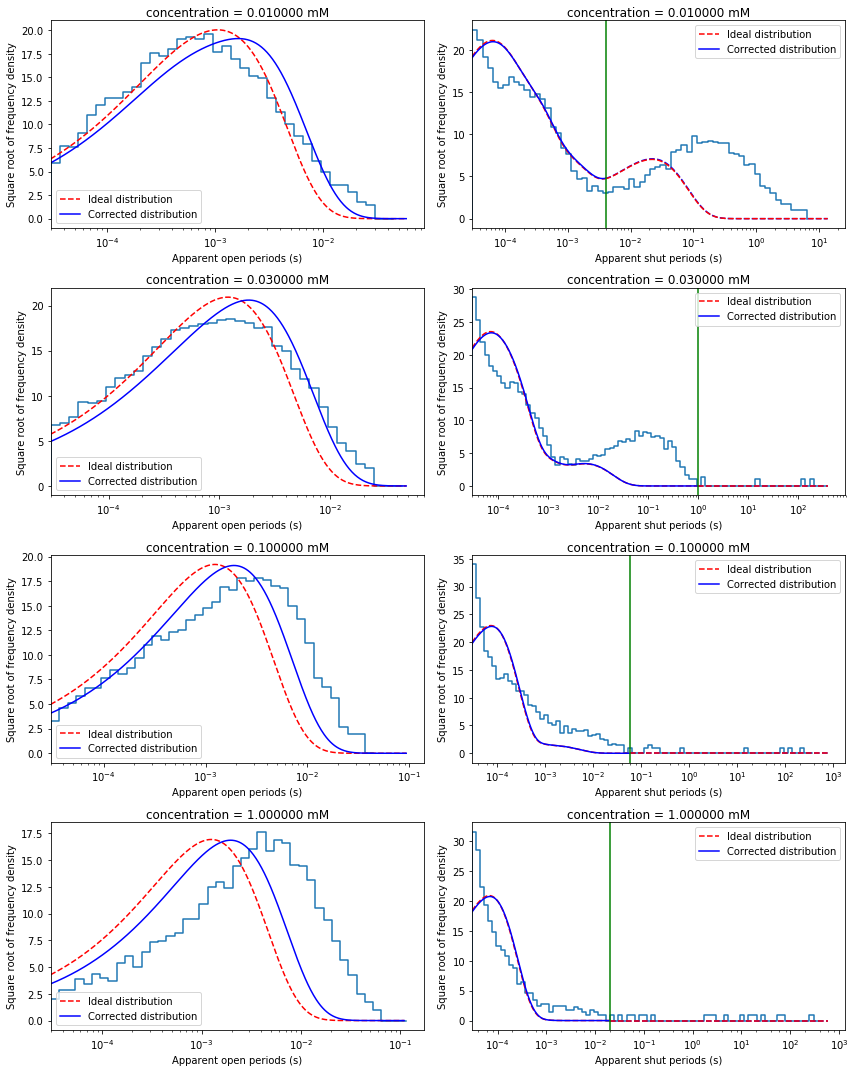
Check data histograms and probability densities calculated from initial guesses¶
Plot dwell-time histograms for inspection. In single-channel analysis field it is common to plot these histograms with x-axis in log scale and y-axis in square-root scale. After such transformation exponential pdf has a bell-shaped form.
Note that to properly overlay ideal and missed-event corrected pdfs ideal pdf has to be scaled (need to renormailse to 1 the area under pdf from \(\tau_{res}\)).
# Scale for ideal pdf
def scalefac(tres, matrix, phiA):
eigs, M = eig(-matrix)
N = inv(M)
k = N.shape[0]
A, w = np.zeros((k, k, k)), np.zeros(k)
for i in range(k):
A[i] = np.dot(M[:, i].reshape(k, 1), N[i].reshape(1, k))
for i in range(k):
w[i] = np.dot(np.dot(np.dot(phiA, A[i]), (-matrix)), np.ones((k, 1)))
return 1 / np.sum((w / eigs) * np.exp(-tres * eigs))
from dcprogs.likelihood import QMatrix
from dcprogs.likelihood import missed_events_pdf, ideal_pdf, IdealG, eig, inv
fig, axes = plt.subplots(len(recs), 2, figsize=(12,15))
for i in range(len(recs)):
mec.set_eff('c', recs[i].conc)
qmatrix = QMatrix(mec.Q, mec.kA)
idealG = IdealG(qmatrix)
# Plot apparent open period histogram
ipdf = ideal_pdf(qmatrix, shut=False)
iscale = scalefac(recs[i].tres, qmatrix.aa, idealG.initial_occupancies)
epdf = missed_events_pdf(qmatrix, recs[i].tres, nmax=2, shut=False)
dcplots.xlog_hist_HJC_fit(axes[i,0], recs[i].tres, recs[i].opint,
epdf, ipdf, iscale, shut=False)
axes[i,0].set_title('concentration = {0:3f} mM'.format(recs[i].conc*1000))
# Plot apparent shut period histogram
ipdf = ideal_pdf(qmatrix, shut=True)
iscale = scalefac(recs[i].tres, qmatrix.ff, idealG.final_occupancies)
epdf = missed_events_pdf(qmatrix, recs[i].tres, nmax=2, shut=True)
dcplots.xlog_hist_HJC_fit(axes[i,1], recs[i].tres, recs[i].shint,
epdf, ipdf, iscale, tcrit=math.fabs(recs[i].tcrit))
axes[i,1].set_title('concentration = {0:6f} mM'.format(recs[i].conc*1000))
fig.tight_layout()
Prepare likelihood function¶
def dcprogslik(x, lik, m, c):
m.theta_unsqueeze(np.exp(x))
l = 0
for i in range(len(c)):
m.set_eff('c', c[i])
l += lik[i](m.Q)
return -l * math.log(10)
def printiter(theta):
global iternum, likelihood, mec, conc
iternum += 1
if iternum % 100 == 0:
lik = dcprogslik(theta, likelihood, mec, conc)
print("iteration # {0:d}; log-lik = {1:.6f}".format(iternum, -lik))
print(np.exp(theta))
# Import HJCFIT likelihood function
from dcprogs.likelihood import Log10Likelihood
kwargs = {'nmax': 2, 'xtol': 1e-12, 'rtol': 1e-12, 'itermax': 100,
'lower_bound': -1e6, 'upper_bound': 0}
likelihood = []
for i in range(len(recs)):
likelihood.append(Log10Likelihood(bursts[i], mec.kA,
recs[i].tres, recs[i].tcrit, **kwargs))
# Extract free parameters
theta = mec.theta()
print ('\ntheta=', theta)
print('Number of free parameters = ', len(theta))
theta= [ 5.00000000e+03 5.00000000e+02 2.70000000e+03 2.00000000e+03
8.00000000e+02 1.50000000e+04 3.00000000e+02 4.50000000e+08
1.50000000e+03 1.20000000e+04 4.00000000e+03 1.20000000e+03
4.50000000e+06 1.00000000e+03]
Number of free parameters = 14
lik = dcprogslik(np.log(theta), likelihood, mec, conc)
print ("\nInitial likelihood = {0:.6f}".format(-lik))
Initial likelihood = 237961.490136
Run optimisation¶
To keep execution time of this notebook short we only run the
optimization for 200 iterations. Change maxiter below for a more
realistic optimisation.
from scipy.optimize import minimize
print ("\nScyPy.minimize (Nelder-Mead) Fitting started: " +
"%4d/%02d/%02d %02d:%02d:%02d"%time.localtime()[0:6])
iternum = 0
start = time.clock()
start_wall = time.time()
maxiter = 200
# maxiter = 30000
result = minimize(dcprogslik, np.log(theta), args=(likelihood, mec, conc), method='Nelder-Mead', callback=printiter,
options={'xtol':1e-5, 'ftol':1e-5, 'maxiter': maxiter, 'maxfev': 150000, 'disp': True})
t3 = time.clock() - start
t3_wall = time.time() - start_wall
print ("\nScyPy.minimize (Nelder-Mead) Fitting finished: " +
"%4d/%02d/%02d %02d:%02d:%02d"%time.localtime()[0:6])
print ('\nCPU time in ScyPy.minimize (Nelder-Mead)=', t3)
print ('Wall clock time in ScyPy.minimize (Nelder-Mead)=', t3_wall)
print ('\nResult ==========================================\n', result)
ScyPy.minimize (Nelder-Mead) Fitting started: 2016/10/28 15:27:05
iteration # 100; log-lik = 263117.756238
[ 5.29171999e+03 3.67684624e+02 1.41434237e+03 8.42349605e+03
8.62838471e+02 5.14562348e+04 3.05197111e+02 5.19871117e+07
2.31972504e+03 2.00532661e+04 4.15472395e+03 5.07080801e+02
5.01742534e+05 8.94263677e+02]
Warning: Maximum number of iterations has been exceeded.
ScyPy.minimize (Nelder-Mead) Fitting finished: 2016/10/28 15:27:15
CPU time in ScyPy.minimize (Nelder-Mead)= 19.19824
Wall clock time in ScyPy.minimize (Nelder-Mead)= 9.663951873779297
Result ==========================================
final_simplex: (array([[ 8.17854356, 6.03708337, 7.10706279, 9.07985218,
6.93061081, 10.98001309, 5.8136173 , 17.23832524,
7.72769902, 9.70103791, 8.19758666, 6.45112468,
13.39684638, 6.95508465],
[ 8.22403089, 6.05593405, 7.12875747, 9.02313412,
6.90356027, 10.95712368, 5.77448477, 17.24438837,
7.73601058, 9.73603764, 8.23203859, 6.49199196,
13.35532125, 6.97085489],
[ 8.27202446, 6.03124292, 7.15576058, 9.10298967,
6.91537324, 10.97906583, 5.87535892, 17.27877025,
7.7104076 , 9.78828276, 8.22704485, 6.37777004,
13.25294199, 6.93122741],
[ 8.32433001, 6.0289382 , 7.1404883 , 9.0383547 ,
6.8205307 , 10.93158792, 5.8308612 , 17.34019634,
7.75095584, 9.72800377, 8.25944946, 6.38964771,
13.31653367, 6.93631765],
[ 8.33985033, 5.92301082, 7.09702954, 9.09805489,
6.89673942, 10.97621154, 5.77517881, 17.32273873,
7.74756632, 9.81249292, 8.25085744, 6.39354715,
13.28852029, 6.94056203],
[ 8.41575544, 5.94125291, 7.19042536, 9.0435014 ,
6.84337862, 10.89976979, 5.76975737, 17.40977212,
7.775724 , 9.77032599, 8.30672733, 6.40129054,
13.28746099, 6.87193334],
[ 8.23460356, 6.06544835, 7.15047868, 9.05344456,
6.87980573, 10.9657658 , 5.76339175, 17.33221254,
7.74893403, 9.78425826, 8.27631384, 6.45009588,
13.17781919, 6.88956063],
[ 8.39823157, 5.92139609, 7.126189 , 9.0460798 ,
6.85351439, 10.9340107 , 5.72892779, 17.42246383,
7.78649285, 9.77082672, 8.31723055, 6.38863181,
13.28356059, 6.92208135],
[ 8.41035142, 6.01081853, 7.19216558, 8.99209568,
6.81683175, 10.90190722, 5.76531268, 17.4582171 ,
7.77716363, 9.72993475, 8.33889227, 6.42272102,
13.29925003, 6.88808181],
[ 8.40340552, 6.0273153 , 7.22178376, 9.03888376,
6.84264901, 10.91086406, 5.79190033, 17.45077881,
7.73933892, 9.80968022, 8.24822381, 6.33622711,
13.28545754, 6.9169019 ],
[ 8.24388707, 6.05157538, 7.20532864, 8.941294 ,
6.84121632, 10.89460159, 5.76758747, 17.41789114,
7.74027848, 9.70505269, 8.28434299, 6.52015363,
13.39744932, 6.94780185],
[ 8.27610963, 6.05970142, 7.18039864, 9.13973644,
6.87300261, 10.92971067, 5.93330882, 17.26117058,
7.73212301, 9.73937094, 8.24832269, 6.4324554 ,
13.1763455 , 6.87493238],
[ 8.38279112, 5.8842607 , 7.13565288, 9.0174619 ,
6.84330267, 10.88373368, 5.78974106, 17.45101242,
7.79970867, 9.74499968, 8.29915767, 6.43571606,
13.37719486, 6.93389061],
[ 8.42420488, 5.88127595, 7.11098537, 9.09632685,
6.83661948, 10.95519365, 5.74824873, 17.27662587,
7.8087689 , 9.797293 , 8.31344718, 6.37128333,
13.36240644, 6.92608137],
[ 8.4266003 , 5.96016415, 7.18559361, 9.00606597,
6.85428849, 10.93451427, 5.8372125 , 17.29392659,
7.78143967, 9.70305234, 8.3055485 , 6.46089968,
13.39443632, 6.98429024]]), array([-263352.60977117, -263336.3471002 , -263329.21681918,
-263318.1251304 , -263309.78955037, -263306.30534451,
-263302.2583715 , -263298.52765242, -263298.30026063,
-263297.42510587, -263292.18626348, -263291.93074637,
-263291.13476093, -263287.65737164, -263287.20390461]))
fun: -263352.60977116873
message: 'Maximum number of iterations has been exceeded.'
nfev: 281
nit: 200
status: 2
success: False
x: array([ 8.17854356, 6.03708337, 7.10706279, 9.07985218,
6.93061081, 10.98001309, 5.8136173 , 17.23832524,
7.72769902, 9.70103791, 8.19758666, 6.45112468,
13.39684638, 6.95508465])
print ("\nFinal likelihood = {0:.16f}".format(-result.fun))
mec.theta_unsqueeze(np.exp(result.x))
print ("\nFinal rate constants:")
mec.printout()
Final likelihood = 263352.6097711687325500
Final rate constants:
class dcpyps.Mechanism
Values of unit rates [1/sec]:
0 From AF* to AF alpha1 3563.66062627
1 From AF to AF* beta1 418.670145871
2 From A2F* to A2F alpha2 1220.55723999
3 From A2F to A2F* beta2 8776.66858648
4 From A3F* to A3F alpha3 1023.11872432
5 From A3F to A3F* beta3 58689.3222512
6 From A3F to A3R gama3 334.828110598
7 From A3R to A3F delta3 64801.2535522
8 From A3F to A2F 3kf(-3) 5448.26105245
9 From A2F to A3F kf(+3) 30655579.3113
10 From A2F to A2R gama2 2270.3721034
11 From A2R to A2F delta2 16334.5522045
12 From A2F to AF 2kf(-2) 3632.17403497
13 From AF to A2F 2kf(+2) 61311158.6227
14 From AF to AR gama1 2368.25771823
15 From AR to AF delta1 633.414278499
16 From A3R to A2R 3k(-3) 3145.40186848
17 From A2R to A3R k(+3) 657925.10102
18 From A2R to AR 2k(-2) 2096.93457899
19 From AR to A2R 2k(+2) 1315850.20204
20 From AR to R k(-1) 1048.46728949
21 From R to AR 3k(+1) 1973775.30306
Conductance of state AF* (pS) = 40
Conductance of state A2F* (pS) = 40
Conductance of state A3F* (pS) = 40
Number of open states = 3
Number of short-lived shut states (within burst) = 6
Number of long-lived shut states (between bursts) = 1
Number of desensitised states = 0
Number of cycles = 2
Cycle 0 is formed of states: A3R A3F A2F A2R
forward product = 5.273692624e+17
backward product = 5.273692624e+17
Cycle 1 is formed of states: AF A2F A2R AR
forward product = 1.848882431e+17
backward product = 1.848882431e+17
Plot experimental histograms and predicted pdfs¶
fig, axes = plt.subplots(len(recs), 2, figsize=(12,15))
for i in range(len(recs)):
mec.set_eff('c', recs[i].conc)
qmatrix = QMatrix(mec.Q, mec.kA)
idealG = IdealG(qmatrix)
# Plot apparent open period histogram
ipdf = ideal_pdf(qmatrix, shut=False)
iscale = scalefac(recs[i].tres, qmatrix.aa, idealG.initial_occupancies)
epdf = missed_events_pdf(qmatrix, recs[i].tres, nmax=2, shut=False)
dcplots.xlog_hist_HJC_fit(axes[i,0], recs[i].tres, recs[i].opint,
epdf, ipdf, iscale, shut=False)
axes[i,0].set_title('concentration = {0:3f} mM'.format(conc[i]*1000))
# Plot apparent shut period histogram
ipdf = ideal_pdf(qmatrix, shut=True)
iscale = scalefac(recs[i].tres, qmatrix.ff, idealG.final_occupancies)
epdf = missed_events_pdf(qmatrix, recs[i].tres, nmax=2, shut=True)
dcplots.xlog_hist_HJC_fit(axes[i,1], recs[i].tres, recs[i].shint,
epdf, ipdf, iscale, tcrit=math.fabs(recs[i].tcrit))
axes[i,1].set_title('concentration = {0:6f} mM'.format(conc[i]*1000))
fig.tight_layout()
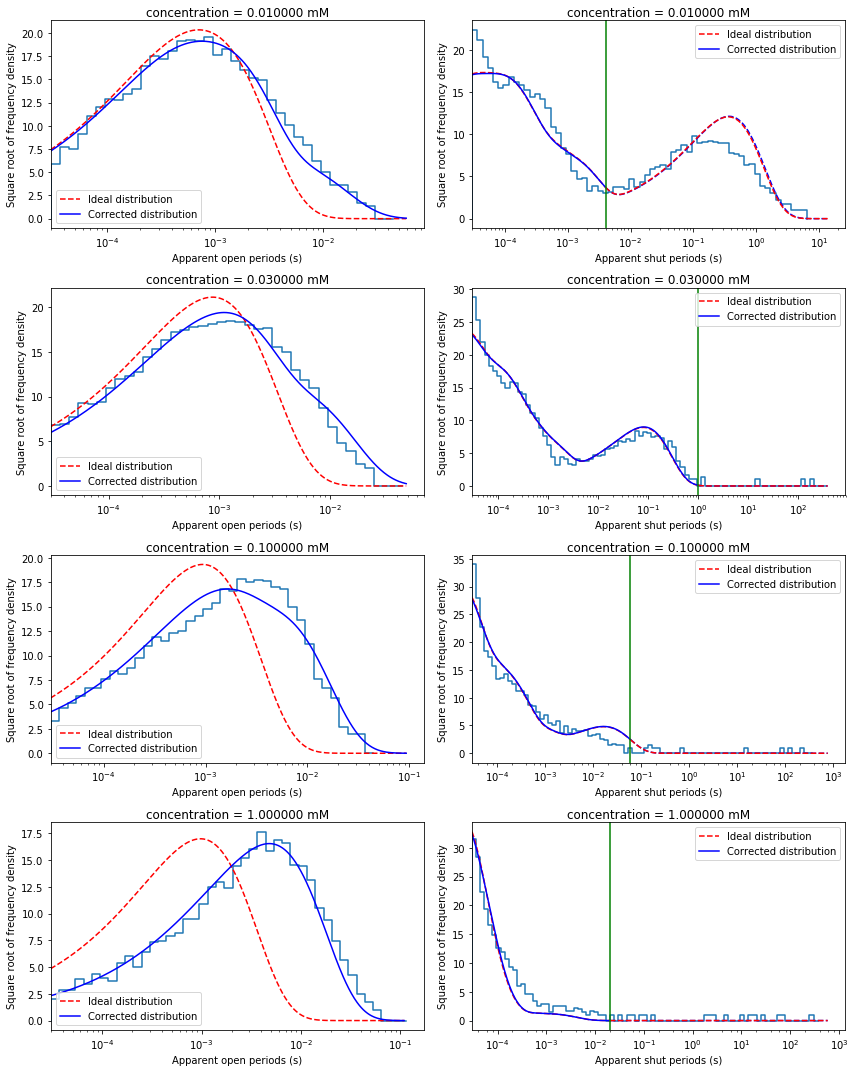
Note that in this record only shut time intervals shorter than critical time (\(t_{crit}\)) were used to minimise likelihood. Thus, only a part of shut time histrogram (to the left from green line, indicating \(t_{crit}\) value, in the above plot) is predicted well by rate constant estimates.