%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from dcprogs.likelihood import DeterminantEq, find_root_intervals, find_roots, QMatrix
from dcprogs.likelihood.random import qmatrix as random_qmatrix
equation = DeterminantEq(random_qmatrix(), 1e-4)
from dcprogs.likelihood import plot_roots
plot_roots(equation, size=25000);
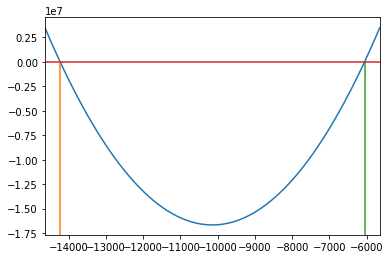
fig, ax = plt.subplots(1,1)
x = np.arange(-10, 0e0, 1e-2)
ax.plot(x, equation(x))
[<matplotlib.lines.Line2D at 0x2baa08f32128>]
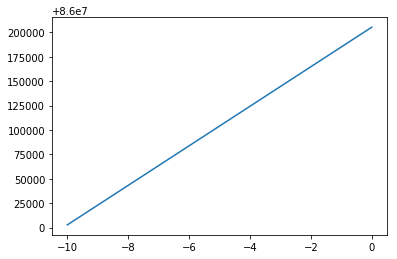
from dcprogs.likelihood import find_root_intervals_brute_force
print(find_root_intervals(equation))
print(find_root_intervals_brute_force(equation, 10))
[((-21337.89286565558, -10668.94643282779), 1), ((-10668.94643282779, 0.0), 1)]
[((-14227.89286565558, -14217.89286565558), 1), ((-6067.89286565558, -6057.89286565558), 1)]
def trial():
from numpy import all
from dcprogs.likelihood import DeterminantEq, find_root_intervals, find_roots, QMatrix
from dcprogs.likelihood.random import qmatrix as random_qmatrix
while True:
#try:
matrix = random_qmatrix()
equation = DeterminantEq(matrix, 1e-4)
return all([r[1] == 1 for r in find_roots(equation)])
#except: continue
print(all([trial() for i in range(500)]))
True
Asymptotic vs Exact for classic Matrix¶
from numpy import array
from dcprogs.likelihood import QMatrix, DeterminantEq, Asymptotes, find_roots
qmatrix = QMatrix(
array([[ -3050, 50, 3000, 0, 0 ],
[ 2./3., -1502./3., 0, 500, 0 ],
[ 15, 0, -2065, 50, 2000 ],
[ 0, 15000, 4000, -19000, 0 ],
[ 0, 0, 10, 0, -10 ] ]), 2)
equation = DeterminantEq(qmatrix, 1e-4)
roots = find_roots(equation)
asymptotes = Asymptotes(equation, roots)
from dcprogs.likelihood import expm, eig, inv
transitions = qmatrix.transpose()
right = eig(transitions.matrix)[1]
eigenvalues = eig(transitions.matrix)[0]
left = eig(transitions.matrix.T)[1].T
tau = 1e-4
af_factor = np.dot(expm(tau * transitions.ff), transitions.fa)
print(af_factor)
print(np.all(abs(af_factor - np.dot(expm(tau * qmatrix.aa), qmatrix.af)) < 1e-8))
for i, j in zip(range(5), [0, 1, 2, 4, 3]):
col = right[:transitions.nopen, i]
row = inv(right)[i, transitions.nopen:]
one_way = np.dot(np.outer(col, row), af_factor)
col = eig(qmatrix.matrix)[1][qmatrix.nopen:, i]
row = inv(eig(qmatrix.matrix)[1])[i, :qmatrix.nopen]
other_way = np.dot(np.outer(col, row), np.dot(expm(tau * qmatrix.aa), qmatrix.af))
print(np.all(abs(one_way - other_way) < 1e-8))
# print i, " is ok", all(abs(np.dot(outer(col, row), af_factor) - ExactG(transitions, 1e-4).D_af(j)) < 1e-8)
# print
# print ExactG(transitions, tau).D_af(i)
[[ 2.21137053e+03 2.09900610e+00 0.00000000e+00]
[ 1.67920488e-01 4.75583079e+02 0.00000000e+00]]
True
True
True
True
True
True
from dcprogs.likelihood import eig, inv
from numpy import exp
from numpy import diag
right = eig(qmatrix.matrix)[1]
eigenvalues = eig(qmatrix.matrix)[0]
# print eigenvalues, "\n"
left = eig(qmatrix.matrix.T)[1].T
indices = [-2, 0, 1, -1, 2]
print(eig(qmatrix.matrix.T)[0][indices])
print(eigenvalues)
print("Same order left and right: ", all(abs(eigenvalues - eig(qmatrix.matrix.T)[0][indices]) < 1e-8))
for eigenvalue, eigenvector in zip(eigenvalues, right.T):
null_mat = qmatrix.matrix - eigenvalue * np.identity(qmatrix.matrix.shape[0])
print("Is right eig: ", all(abs(np.dot(null_mat, eigenvector)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eig(qmatrix.matrix.T)[0], left):
null_mat = qmatrix.matrix - eigenvalue * np.identity(qmatrix.matrix.shape[0])
print("Is left eig: ", all(abs(np.dot(eigenvector, null_mat)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eigenvalues, inv(right)):
null_mat = qmatrix.matrix - eigenvalue * np.identity(qmatrix.matrix.shape[0])
print("Is row of inv(right) a left eigenvector: ", all(abs(np.dot(eigenvector, null_mat)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eigenvalues, inv(left).T):
null_mat = qmatrix.matrix - eigenvalue * np.identity(qmatrix.matrix.shape[0])
print("Is column of inv(left) a right eigenvector: ", all(abs(np.dot(null_mat, eigenvector)) < 1e-8), eigenvalue)
[ -1.94082023e+04 -3.09352724e+03 -2.02211927e+03 -1.01817905e+02
-3.97221336e-14]
[ -1.94082023e+04 -3.09352724e+03 -2.02211927e+03 -1.01817905e+02
-3.41740525e-14]
Same order left and right: True
Is right eig: True -19408.2022554
Is right eig: True -3093.52723698
Is right eig: True -2022.1192695
Is right eig: True -101.8179048
Is right eig: True -3.41740524716e-14
Is left eig: True -3093.52723698
Is left eig: True -2022.1192695
Is left eig: True -3.97221336337e-14
Is left eig: True -19408.2022554
Is left eig: True -101.8179048
Is row of inv(right) a left eigenvector: True -19408.2022554
Is row of inv(right) a left eigenvector: True -3093.52723698
Is row of inv(right) a left eigenvector: True -2022.1192695
Is row of inv(right) a left eigenvector: True -101.8179048
Is row of inv(right) a left eigenvector: True -3.41740524716e-14
Is column of inv(left) a right eigenvector: False -19408.2022554
Is column of inv(left) a right eigenvector: False -3093.52723698
Is column of inv(left) a right eigenvector: False -2022.1192695
Is column of inv(left) a right eigenvector: False -101.8179048
Is column of inv(left) a right eigenvector: False -3.41740524716e-14
from numpy.linalg import eig, inv
from dcprogs.likelihood import eig as dceig
from dcprogs.likelihood import inv as dcinv
from numpy import exp
from numpy import diag
Qmatrix2 = qmatrix.transpose()
try:
right = eig(Qmatrix2.matrix)[1]
eigenvalues = eig(Qmatrix2.matrix)[0]
eigenvaluesT = eig(Qmatrix2.matrix.T)[0]
left = eig(Qmatrix2.matrix.T)[1].T
invmat = inv(right)
invmatL = inv(left).T
except: #fallback for longdoubles to eigen
right = dceig(Qmatrix2.matrix)[1]
eigenvalues = dceig(Qmatrix2.matrix)[0]
left = dceig(Qmatrix2.matrix.T)[1].T
eigenvaluesT = dceig(Qmatrix2.matrix.T)[0]
invmat = dcinv(right)
invmatL = dcinv(left).T
print("Same order left and right: ", all(abs(eigenvalues - eigenvaluesT) < 1e-8))
for eigenvalue, eigenvector in zip(eigenvalues, right.T):
null_mat = Qmatrix2.matrix - eigenvalue * np.identity(Qmatrix2.matrix.shape[0])
print("Is right eig: ", all(abs(np.dot(null_mat, eigenvector)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eigenvalues, left):
null_mat = Qmatrix2.matrix - eigenvalue * np.identity(Qmatrix2.matrix.shape[0])
print("Is left eig: ", all(abs(np.dot(eigenvector, null_mat)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eigenvalues, invmat):
null_mat = Qmatrix2.matrix - eigenvalue * np.identity(Qmatrix2.matrix.shape[0])
print("Is row of inv(right) a left eigenvector: ", all(abs(np.dot(eigenvector, null_mat)) < 1e-8), eigenvalue)
for eigenvalue, eigenvector in zip(eigenvalues, invmatL):
null_mat = Qmatrix2.matrix - eigenvalue * np.identity(Qmatrix2.matrix.shape[0])
print("Is column of inv(left) a right eigenvector: ", all(abs(np.dot(null_mat, eigenvector)) < 1e-8), eigenvalue)
Same order left and right: False
Is right eig: True -19408.2022554
Is right eig: True -3093.52723698
Is right eig: True -2022.1192695
Is right eig: True -101.8179048
Is right eig: True -1.09178364675e-16
Is left eig: True -19408.2022554
Is left eig: True -3093.52723698
Is left eig: True -2022.1192695
Is left eig: False -101.8179048
Is left eig: False -1.09178364675e-16
Is row of inv(right) a left eigenvector: True -19408.2022554
Is row of inv(right) a left eigenvector: True -3093.52723698
Is row of inv(right) a left eigenvector: True -2022.1192695
Is row of inv(right) a left eigenvector: True -101.8179048
Is row of inv(right) a left eigenvector: True -1.09178364675e-16
Is column of inv(left) a right eigenvector: True -19408.2022554
Is column of inv(left) a right eigenvector: True -3093.52723698
Is column of inv(left) a right eigenvector: True -2022.1192695
Is column of inv(left) a right eigenvector: False -101.8179048
Is column of inv(left) a right eigenvector: False -1.09178364675e-16
from numpy import array
from dcprogs.likelihood import QMatrix, DeterminantEq, Asymptotes, find_roots, ExactSurvivor
qmatrix = QMatrix(
array([[ -3050, 50, 3000, 0, 0 ],
[ 2./3., -1502./3., 0, 500, 0 ],
[ 15, 0, -2065, 50, 2000 ],
[ 0, 15000, 4000, -19000, 0 ],
[ 0, 0, 10, 0, -10 ] ]), 2)
transitions = qmatrix.transpose()
tau = 1e-4
exact = ExactSurvivor(transitions, tau)
equation = DeterminantEq(transitions, tau)
roots = find_roots(equation)
approx = Asymptotes(equation, roots)
try:
eigenvalues = eig(-transitions.matrix)[0]
except:
eigenvalues = dceig(-transitions.matrix)[0]
def C_i10(i):
from numpy import zeros
result = zeros((transitions.nopen, transitions.nopen), dtype='float64')
for j in range(transitions.matrix.shape[0]):
if i == j: continue
result += np.dot(exact.D_af(i), exact.recursion_af(j, 0, 0)) / (eigenvalues[j] - eigenvalues[i])
result -= np.dot(exact.D_af(j), exact.recursion_af(i, 0, 0)) / (eigenvalues[i] - eigenvalues[j])
return result
def C_i20(i):
from numpy import zeros
result = zeros((transitions.nopen, transitions.nopen), dtype='float64')
for j in range(transitions.matrix.shape[0]):
if i == j: continue
result += ( np.dot(exact.D_af(i), exact.recursion_af(j, 1, 0))
+ np.dot(exact.D_af(j), exact.recursion_af(i, 1, 0)) ) / (eigenvalues[j] - eigenvalues[i])
result += ( np.dot(exact.D_af(i), exact.recursion_af(j, 1, 1))
- np.dot(exact.D_af(j), exact.recursion_af(i, 1, 1)) ) / (eigenvalues[j] - eigenvalues[i])**2
return result
def C_i21(i):
result = np.dot(exact.D_af(i), exact.recursion_af(i, 1, 0))
for j in range(transitions.matrix.shape[0]):
if i == j: continue
result -= np.dot(exact.D_af(j), exact.recursion_af(i, 1, 1)) / (eigenvalues[i] - eigenvalues[j])
return result
def C_i22(i): return np.dot(exact.D_af(i), exact.recursion_af(i, 1, 1)) * 0.5
print(np.all([np.all(abs(C_i10(i) - exact.recursion_af(i, 1, 0)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i20(i) - exact.recursion_af(i, 2, 0)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i21(i) - exact.recursion_af(i, 2, 1)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i22(i) - exact.recursion_af(i, 2, 2)) < 1e-8) for i in range(5)]))
print(C_i22(0))
print(exact.recursion_af(0, 2, 2))
#print np.dot(exact.D_af(1) * exact.recursion_af(1, 1, 1)
True
True
True
True
[[ 4.44037679e+01 -1.92479231e+02 -4.57813227e+00]
[ -1.53983385e+04 6.67479474e+04 1.58760470e+03]
[ -2.28906614e-02 9.92252936e-02 2.36008070e-03]]
[[ 4.44037679e+01 -1.92479231e+02 -4.57813227e+00]
[ -1.53983385e+04 6.67479474e+04 1.58760470e+03]
[ -2.28906614e-02 9.92252936e-02 2.36008070e-03]]