Exact Survivor Function¶

This is equation 3.12 from Hawkes, Jalali, Colqhoun (1990). A simpler form is also given in Colquhoun, Hawkes and Srodzinski (1996).

These equations were performed in two parts:

the recurrence on the one side (recursion_formula.h). It is a set of template functions. This means it can be tested more simply on scalars (rather than matrices, as in the paper), as is done in tests/recursion_formula.cc.
the acrutal survivor functions \(^{A}R(t)\) and \(^{F}R(t)\) are implemented as instances of exact_survivor.cc:ExactSurvivor::RecursionInterface.

Checking the implementation¶

The classic \(Q\) matrix first:

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

from numpy import array
from dcprogs.likelihood import QMatrix, DeterminantEq, Asymptotes, find_roots, ExactSurvivor
qmatrix = QMatrix(
           array([[ -3050,        50,  3000,      0,    0 ],
                  [ 2./3., -1502./3.,     0,    500,    0 ],
                  [    15,         0, -2065,     50, 2000 ],
                  [     0,     15000,  4000, -19000,    0 ],
                  [     0,         0,    10,      0,  -10 ] ]), 2)

Then compares a few recursion terms by hand and by c++

from numpy import array
from dcprogs.likelihood import QMatrix, DeterminantEq, Asymptotes, find_roots, ExactSurvivor, eig
qmatrix = QMatrix(
           array([[ -3050,        50,  3000,      0,    0 ],
                  [ 2./3., -1502./3.,     0,    500,    0 ],
                  [    15,         0, -2065,     50, 2000 ],
                  [     0,     15000,  4000, -19000,    0 ],
                  [     0,         0,    10,      0,  -10 ] ]), 2)

transitions = qmatrix.transpose()
tau = 1e-4
exact = ExactSurvivor(transitions, tau)
equation = DeterminantEq(transitions, tau)
roots = find_roots(equation)
approx = Asymptotes(equation, roots)
eigenvalues = eig(-transitions.matrix)[0]

def C_i10(i):
    from numpy import zeros
    result = zeros((transitions.nopen, transitions.nopen), dtype='float64')
    for j in range(transitions.matrix.shape[0]):
        if i == j: continue
        result += np.dot(exact.D_af(i), exact.recursion_af(j, 0, 0)) / (eigenvalues[j] - eigenvalues[i])
        result -= np.dot(exact.D_af(j), exact.recursion_af(i, 0, 0)) / (eigenvalues[i] - eigenvalues[j])
    return result

def C_i20(i):
    from numpy import zeros
    result = zeros((transitions.nopen, transitions.nopen), dtype='float64')
    for j in range(transitions.matrix.shape[0]):
        if i == j: continue
        result += ( np.dot(exact.D_af(i), exact.recursion_af(j, 1, 0))
                    + np.dot(exact.D_af(j), exact.recursion_af(i, 1, 0)) ) / (eigenvalues[j] - eigenvalues[i])
        result += ( np.dot(exact.D_af(i), exact.recursion_af(j, 1, 1))
                    - np.dot(exact.D_af(j), exact.recursion_af(i, 1, 1)) ) / (eigenvalues[j] - eigenvalues[i])**2
    return result

def C_i21(i):
    result = np.dot(exact.D_af(i), exact.recursion_af(i, 1, 0))
    for j in range(transitions.matrix.shape[0]):
        if i == j: continue
        result -= np.dot(exact.D_af(j), exact.recursion_af(i, 1, 1)) / (eigenvalues[i] - eigenvalues[j])
    return result

def C_i22(i): return np.dot(exact.D_af(i), exact.recursion_af(i, 1, 1)) * 0.5

print(np.all([np.all(abs(C_i10(i) - exact.recursion_af(i, 1, 0)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i20(i) - exact.recursion_af(i, 2, 0)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i21(i) - exact.recursion_af(i, 2, 1)) < 1e-8) for i in range(5)]))
print(np.all([np.all(abs(C_i22(i) - exact.recursion_af(i, 2, 2)) < 1e-8) for i in range(5)]))

True
True
True
True

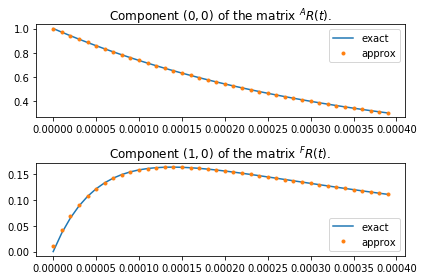
Try and compare exact and approx via plot. The following is for \(^{A}R(t)\) and \(^{F}R(t)\).

tau, i, j, n = 1e-4, 0, 0, 4

fig, ax = plt.subplots(2, 1)

transitions = qmatrix
exact = ExactSurvivor(transitions, tau)
equation = DeterminantEq(transitions, tau)
roots = find_roots(equation)
approx = Asymptotes(equation, roots)

x = np.arange(0, n * tau, tau / 10.)
ax[0].plot(x, exact.af(x)[:, i, j], label="exact")
ax[0].plot(x, approx(x)[:, i, j], '.', label="approx")
ax[0].set_title("Component ${0}$ of the matrix $^{{A}}R(t)$.".format((i, j)))
ax[0].legend()

roots = find_roots(equation.transpose())
approx = Asymptotes(equation.transpose(), roots)

i, j = 1, 0
x = np.arange(0, n*tau, tau / 10.)
ax[1].plot(x, exact.fa(x)[:, i, j], label="exact")
ax[1].plot(x, approx(x)[:, i, j], '.', label="approx")
ax[1].set_title("Component ${0}$ of the matrix $^{{F}}R(t)$.".format((i, j)))
ax[1].legend(loc=0)

fig.tight_layout()