Distribution histograms and individual benchmarks¶
%matplotlib inline
This notebook mainly serves to extract data used for the Archer eCSE report.
Set the number of OpenMP threads to use. Note that the number of threads is fixed at import time of DCPROGS so you will need to change restart the notebook and reexecute from the begining for any changes to take effect.
import os
os.environ['OMP_NUM_THREADS'] = '1'
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.text as mtext
import time
import math
import sys
import numpy as np
from scipy.optimize import minimize
from dcpyps import dcio
from dcpyps import dataset
from dcpyps import mechanism
from dcprogs.likelihood import Log10Likelihood
# LOAD DATA: Burzomato 2004 example set.
scnfiles = [["./samples/glydemo/A-10.scn"],
["./samples/glydemo/B-30.scn"],
["./samples/glydemo/C-100.scn"],
["./samples/glydemo/D-1000.scn"]]
tres = [0.000030, 0.000030, 0.000030, 0.000030]
tcrit = [0.004, -1, -0.06, -0.02]
conc = [10e-6, 30e-6, 100e-6, 1000e-6]
recs = []
bursts = []
for i in range(len(scnfiles)):
rec = dataset.SCRecord(scnfiles[i], conc[i], tres[i], tcrit[i])
rec.record_type = 'recorded'
recs.append(rec)
bursts.append(rec.bursts.intervals())
n_experiments = len(recs)
openings = []
opening_dists = []
n_bursts = np.empty(4)
for i,rec in enumerate(recs):
n_bursts[i] = rec.bursts.count()
openings = np.zeros(rec.bursts.count())
for i,burst in enumerate(rec.bursts.all()):
openings[i] = burst.get_openings_number()
opening_dists.append(openings)
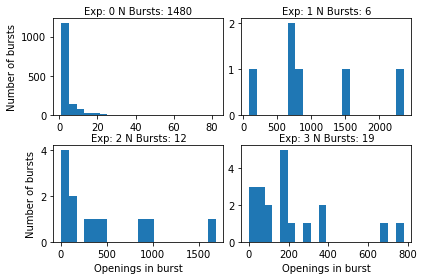
Plot the distribution of bursts within the 4 different experiments showing how number of bursts corelate with the lenght of the bursts.
fig, ax = plt.subplots(2,2)
ax = ax.flatten()
for i in range(n_experiments):
ax[i].hist(opening_dists[i], bins=20)
ax[i].set_title("Exp: {} N Bursts: {}".format(i, int(n_bursts[i])), fontsize=10)
ylabel = ax[0].set_ylabel('Number of bursts')
ylabel = ax[2].set_ylabel('Number of bursts')
xlabel = ax[2].set_xlabel('Openings in burst')
xlabel = ax[3].set_xlabel('Openings in burst')
fig.tight_layout(w_pad=0.1, h_pad=0.1)
# LOAD FLIP MECHANISM USED Burzomato et al 2004
mecfn = "./samples/mec/demomec.mec"
version, meclist, max_mecnum = dcio.mec_get_list(mecfn)
mec = dcio.mec_load(mecfn, meclist[2][0])
# PREPARE RATE CONSTANTS.
rates = [4500.0, 700.0, 2500.0, 1800.0, 900.0, 18000.0, 200.0, 0.1100E+06, 4900.0, 0.4000E+09, 1850.0, 10000.0, 5000.0, 0.7500E+09, 8500.0, 1050.0, 3500.0, 0.5000E+07, 2300.0, 0.9500E+07, 1950, 0.130000E+08]
mec.set_rateconstants(rates)
# Fixed rates.
#fixed = np.array([False, False, False, False, False, False, False, True,
# False, False, False, False, False, False])
#if fixed.size == len(mec.Rates):
for i in range(len(mec.Rates)):
mec.Rates[i].fixed = False
# Constrained rates.
mec.Rates[21].is_constrained = True
mec.Rates[21].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[21].constrain_args = [17, 3]
mec.Rates[19].is_constrained = True
mec.Rates[19].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[19].constrain_args = [17, 2]
mec.Rates[16].is_constrained = True
mec.Rates[16].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[16].constrain_args = [20, 3]
mec.Rates[18].is_constrained = True
mec.Rates[18].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[18].constrain_args = [20, 2]
mec.Rates[8].is_constrained = True
mec.Rates[8].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[8].constrain_args = [12, 1.5]
mec.Rates[13].is_constrained = True
mec.Rates[13].constrain_func = mechanism.constrain_rate_multiple
mec.Rates[13].constrain_args = [9, 2]
mec.update_constrains()
mec.set_mr(True, 7, 0)
mec.set_mr(True, 15, 1)
mec.printout(sys.stdout)
theta = np.log(mec.theta())
kwargs = {'nmax': 2, 'xtol': 1e-12, 'rtol': 1e-12, 'itermax': 100,
'lower_bound': -1e6, 'upper_bound': 0}
likelihood = []
for i in range(len(recs)):
likelihood.append(Log10Likelihood(bursts[i], mec.kA,
recs[i].tres, recs[i].tcrit, **kwargs))
def dcprogslik(x, args=None):
mec.theta_unsqueeze(np.exp(x))
lik = 0
for i in range(len(conc)):
mec.set_eff('c', conc[i])
lik += -likelihood[i](mec.Q) * math.log(10)
return lik
class dcpyps.Mechanism
Values of unit rates [1/sec]:
0 From AF* to AF alpha1 4500.0
1 From AF to AF* beta1 700.0
2 From A2F* to A2F alpha2 2500.0
3 From A2F to A2F* beta2 1800.0
4 From A3F* to A3F alpha3 900.0
5 From A3F to A3F* beta3 18000.0
6 From A3F to A3R gama3 200.0
7 From A3R to A3F delta3 67459.4594595
8 From A3F to A2F 3kf(-3) 7500.0
9 From A2F to A3F kf(+3) 400000000.0
10 From A2F to A2R gama2 1850.0
11 From A2R to A2F delta2 10000.0
12 From A2F to AF 2kf(-2) 5000.0
13 From AF to A2F 2kf(+2) 800000000.0
14 From AF to AR gama1 8500.0
15 From AR to AF delta1 736.313236313
16 From A3R to A2R 3k(-3) 5850
17 From A2R to A3R k(+3) 5000000.0
18 From A2R to AR 2k(-2) 3900
19 From AR to A2R 2k(+2) 10000000.0
20 From AR to R k(-1) 1950
21 From R to AR 3k(+1) 15000000.0
Conductance of state AF* (pS) = 40
Conductance of state A2F* (pS) = 40
Conductance of state A3F* (pS) = 40
Number of open states = 3
Number of short-lived shut states (within burst) = 6
Number of long-lived shut states (between bursts) = 1
Number of desensitised states = 0
Number of cycles = 2
Cycle 0 is formed of states: A3R A3F A2F A2R
forward product = 4.680000000e+18
backward product = 4.680000000e+18
Cycle 1 is formed of states: AF A2F A2R AR
forward product = 4.250000000e+18
backward product = 4.250000000e+18
%%timeit
dcprogslik(theta)
10 loops, best of 3: 39.1 ms per loop
%%timeit
i = 0
mec.set_eff('c', conc[i])
lik = -likelihood[i](mec.Q) * math.log(10)
100 loops, best of 3: 8.65 ms per loop
%%timeit
i = 1
mec.set_eff('c', conc[i])
lik = -likelihood[i](mec.Q) * math.log(10)
100 loops, best of 3: 10.6 ms per loop
%%timeit
i = 2
mec.set_eff('c', conc[i])
lik = -likelihood[i](mec.Q) * math.log(10)
100 loops, best of 3: 9 ms per loop
%%timeit
i = 3
mec.set_eff('c', conc[i])
lik = -likelihood[i](mec.Q) * math.log(10)
100 loops, best of 3: 7.72 ms per loop